DI LUCA ELETTRICO
Sì, avete letto bene. Anche gli uccelli rispettano la legge. Ma di quali leggi stiamo parlando? Facciamo un passo indietro.
I biologi non amano la matematica. O almeno questa era la mia impressione. Eppure, se anche voi avete intrapreso un percorso di studi in questo ambito (o conoscete qualcuno che lo ha fatto), vi sarete resi conto che la biologia si è evoluta nel tempo per diventare sempre più costellata di numeri e formule. Biostatistica, biofisica, bioinformatica: tutte discipline che rimandano all’idea che non si possa più ritenere di comprendere a fondo la Vita se non attraverso una lente matematica, fatta di approcci quantitativi. Certamente non si devono trascurare metodi descrittivi e qualitativi, ma questi devono essere affiancati e supportati da misurazioni precise e quantità. In poche parole, la biologia si è fatta scienza esatta. O quasi…
D’accordo, è arrivato il momento di proporre un esempio per capire di cosa sto parlando. E per farlo vi racconterò una storia!
Il protagonista di questa storia si chiama Vilfredo Pareto. Siamo nella seconda metà dell’Ottocento, periodo dominato dalla corrente di pensiero del Positivismo, che sosteneva che l’unico metodo valido per conoscere e descrivere la realtà fosse quello scientifico. Pareto era figlio del suo tempo, infatti viene ricordato ancora oggi come colui che aprì le porte dell’economia e della sociologia alla matematica. Nelle sue opere egli sosteneva che anche discipline come quella economica avessero la dignità di scienze esatte, al pari della fisica e della matematica, appunto. Tralasciando la sua ideologia politica (che meriterebbe una riflessione a parte), di tutta la sua vasta attività intellettuale una intuizione in particolare rimane tutt’ora intrigante, a mio parere. Mi riferisco alla nota “legge di Pareto”.
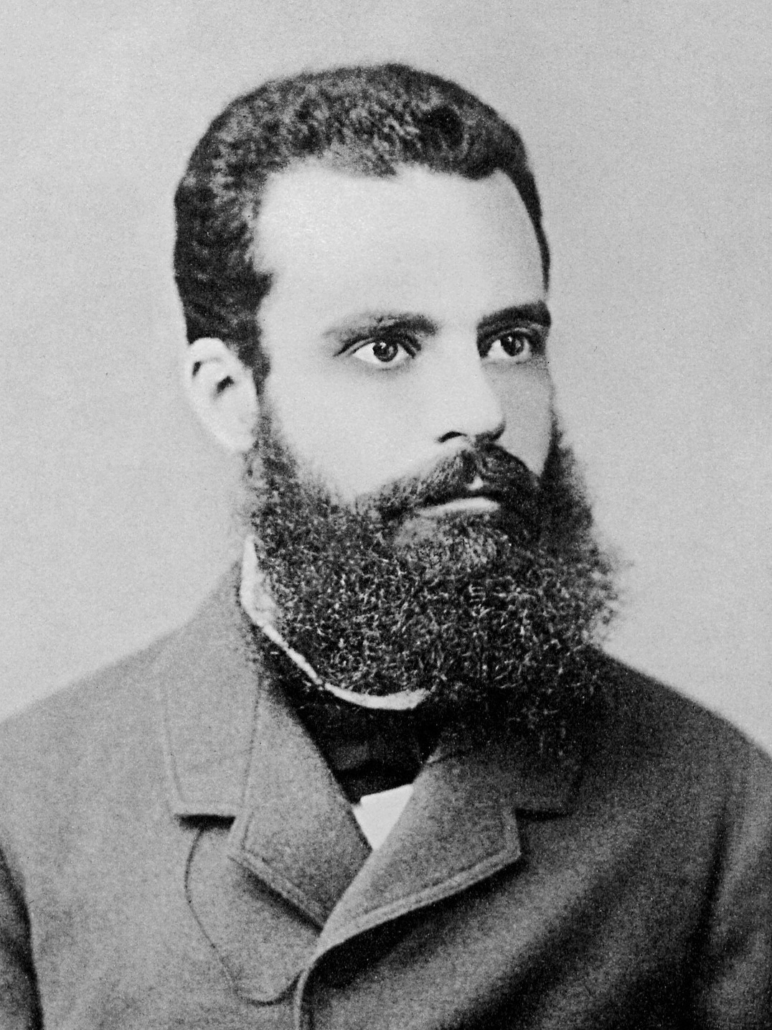
Si racconta che il nostro buon vecchio Vilfredo stesse contemplando il suo orticello di casa, quando notò un fatto ricorrente nei suoi ortaggi. Si rese conto che la maggior parte dei piselli che riusciva a raccogliere veniva prodotta da una porzione ristretta di baccelli. In particolare, si mise a fare i conti e osservò che l’80% dei piselli proveniva dal 20% dei baccelli. Che occhio attento! Da questa prima constatazione egli estrapolò una legge più generale che poteva essere applicata anche ad altri contesti reali. Per esempio, essendo egli particolarmente interessato alle disparità economiche nella popolazione, dimostrò che in Italia in quel momento la maggior parte delle ricchezze era posseduta da una cerchia ristretta di persone. E anche qui ritornava il rapporto 80/20: l’80% delle terre era in mano al 20% degli individui. Una sproporzione notevole, su cui potremmo soffermarci a lungo per dibattere di giustizia sociale… Ma non è questo l’obiettivo del racconto di oggi, caro lettore. Vorrei attirare la tua attenzione su questo altro aspetto: da una semplice osservazione del proprio giardino Pareto ha messo in atto un processo complesso di generalizzazione per arrivare alla conclusione che lo sbilanciamento valido per i suoi legumi potesse avere un senso anche in molti altri contesti della realtà in cui viviamo. Sembra quasi un discorso filosofico… e infatti lo è! Ci torneremo più avanti.
A partire da questa prima intuizione, sempre più fenomeni furono studiati con l’idea che si potesse applicare la legge 80/20. Ne esistono dei più disparati, e alcuni sono proprio curiosi! Per esempio, gli esperti di informatica ci dicono che l’80% dei visitatori di un sito web vede solo il 20% delle pagine. E qualche economista sostiene anche che l’80% delle lamentele rivolte alle aziende provenga solo dal 20% dei rispettivi clienti [1]. Ovviamente, i valori 80 e 20 sono puramente indicativi. Infatti sono ottenuti tramite osservazioni empiriche, cioè valutazioni che si basano su situazioni precise riscontrate in casi particolari. Quindi bisogna considerarli approssimativi. Ma ciò non ci deve indurre a pensare che tutto il discorso sulla legge di Pareto sia una frottola. D’altronde, se invece che 80/20 fosse 70/30, non saremmo forse comunque stupiti dalla regolarità con cui questi numeri si ripresentano? Al di là dei valori specifici, la nostra sorpresa deriva dal fatto che il mondo segua delle regole così chiare e ricorrenti.
Ma torniamo ai nostri uccelli, quelli del titolo. In uno studio del 2014 alcuni ricercatori hanno analizzato i dati relativi alle attività di birdwatching nello stato di New York [2]. In particolare, si sono soffermati sulle proporzioni delle specie osservate in varie località e in varie annate. Indovinate un po’? È emerso che l’80% degli esemplari contati apparteneva al 20% delle specie totali osservate. In altri termini, la maggior parte dei volatili avvistati faceva parte di poche specie molto ricorrenti. Coincidenze? Non credo. In natura, infatti, sono numerosi i contesti in cui è valida questa legge. Si è stimato che il 20% delle specie animali e vegetali contribuiscano per l’80% alla biomassa del pianeta. E anche che l’80% delle prede venga cacciata dal 20% dei predatori [3]. E così via.

A questo punto del racconto, possiamo affermare che ci sia un filo rosso che lega tutto il mondo che ci circonda in modo indissolubile. Che si tratti di esseri umani in lotta per le risorse economiche o di animali alla ricerca di cibo, la legge di Pareto rappresenta un principio fondamentale che governa la competizione tra individui. E, come si può facilmente immaginare, poiché le risorse spesso scarseggiano la distribuzione finale è sproporzionata, sbilanciata.
Dalla legge di Pareto, nella sua formulazione basilare, derivano concetti più complessi quali l’ottimo paretiano e la distribuzione paretiana. Tranquillo, caro lettore, non sta per iniziare una lezione universitaria di economia e statistica! Ma con alcuni esempi tratti dalla biologia ti convincerò che anche in questo caso la natura segue regole assai precise.
Un sistema è considerato ottimale in senso paretiano quando la distribuzione di risorse è la migliore possibile. In particolare, si è raggiunto il punto ottimale quando non si può migliorare ulteriormente la condizione di un soggetto senza peggiorare la condizione di un altro. Per esempio, pensiamo ad una rete stradale: bisogna bilanciare il numero di svincoli e di strade da costruire – che impattano sul costo di costruzione e manutenzione – con le distanze tra i vari nodi centrali, che influiscono sulla rapidità degli spostamenti. In poche parole, la situazione ottimale si ha quando si può spendere poco per costruire e mantenere la rete, garantendo però al contempo un collegamento rapido ed efficiente tra i vari punti. I nostri neuroni funzionano allo stesso modo [4]. Per trasmettere impulsi elettrici da una zona del cervello all’altra creano un vero e proprio circuito, che deve essere il più efficiente possibile. E si è dimostrato che queste meticolose regole di collegamento vengono seguite anche dalle piante quando generano nuove radici e nuovi rami. Insomma, la natura è piena di strutture ramificate, e tutte rispettano gli stessi principi di design, per così dire. È una questione di allocazione delle risorse. Affascinante, vero?
Ma non finisce qui!
Anche l’evoluzione degli esseri viventi deve sottostare a proporzioni ben definite. Proviamo a fare un esercizio di immaginazione: nel mondo animale esistono forse tutte le possibili combinazioni di forme, dimensioni, colori? Oppure alcuni tratti sono più comuni di altri? Neanche a dirlo, l’evoluzione segue il principio di Pareto, come dimostrato da alcuni studi sugli uccelli (sì, sempre loro!). La forma e la dimensione del becco devono essere le migliori per riuscire a trovare cibo, ma non devono mettere a repentaglio l’agilità nei movimenti: ecco, quindi, che non esisteranno piccoli fringuelli con becchi giganti, perché sarebbero troppo goffi nel volo ed inesorabilmente esposti a predatori affamati… L’evoluzione selezionerà la migliore proporzione per garantire un risultato ottimale. Esempi simili riguardano la forma dei denti dei roditori [5]; le strategie di sopravvivenza dei microrganismi in fasi di abbondanza di cibo o, al contrario, in assenza di risorse [5]; il rapporto tra la massa corporea e la longevità dei mammiferi [6]; la diffusione delle infezioni di malaria [7]. Insomma, Vilfredo Pareto ci aveva visto lungo con la sua intuizione.

La legge di Pareto sembra quindi avere il valore di legge universale, ovvero capace di unificare i fenomeni del reale sotto un’unica spiegazione. È piuttosto ambiziosa come pretesa, vero? Ma non deve stupirci. Che all’essere umano sia sempre piaciuto trovare leggi che descrivono la realtà, lo dimostrano i diversi libri intitolati più o meno così: «Le 10 formule che hanno cambiato la storia», o ancora «Le 5 equazioni che hanno cambiato il mondo». E non ti sorprenderà, caro lettore, che tra queste potenti leggi matematiche si annoverino teorie rivoluzionarie come la gravitazione universale e la relatività di Einstein (E = mc2 ti dice qualcosa?). Ma anche restando a formule più semplici, sono sicuro che tutti abbiamo ripetuto almeno una volta il famoso teorema di Pitagora: i quadrati costruiti sui cateti sono pari al quadrato dell’ipotenusa… Newton, Einstein, Pitagora, e tutti gli altri esseri umani che riuscirono a decifrare uno dei meccanismi segreti dell’universo, avevano una caratteristica in comune: la capacità di meravigliarsi di fronte ai fenomeni naturali. Ma non si fermavano ad osservare! Si ostinavano a cercare un modo per spiegare il mondo, riassumendolo in una formula, spesso non molto complicata, allettati dall’idea di poter semplificare fenomeni così complessi. D’altronde, i grandi pensatori sapevano che con ogni nuova legge matematica l’essere umano espande la propria comprensione del mondo e tenta di abbracciare l’infinito. O almeno ci prova!
Tutto molto bello, fino a qui. Ma ora veniamo agli avvertimenti. Da un lato l’essere umano dimostra una tensione verso la comprensione totale della realtà, intesa come un’entità uniforme e ordinata: questo ci fa onore, e ci rende dei veri sognatori. Tuttavia, non bisogna rimanere impantanati nella convinzione che tutto possa essere spiegato con una formula o un’etichetta. È allettante, ma al contempo limitante. Lo sanno bene i biologi evoluzionisti, cioè coloro che studiano come gli essere viventi siano cambiati nel corso della storia adattandosi di volta in volta a nuovi ambienti. E in particolare gli esperti di tassonomia, ovvero gli scienziati che hanno ideato e aggiornato le regole con cui si attribuiscono i nomi ad animali, piante, funghi, batteri, e così via. La nomenclatura proposta da Linneo nel Settecento – per intenderci, quella con due parole in latino, per cui il vostro adorato gatto si chiamerà Felis catus – non teneva conto di nuove scoperte sul concetto di specie che sarebbero emerse nei secoli successivi. Ecco perché spesso i nomi scientifici vengono modificati, adattati o sostituiti completamente. Comunque non è tutta colpa di Linneo, sono passati circa trecento anni dalla sua idea… Insomma, adoriamo creare categorie, dare etichette, schematizzare. E questo ci facilita lo studio e la memorizzazione delle bizzarrie della realtà. Ma a volte perdiamo di vista il senso vero delle cose, con la loro profondità e le svariate sfumature.
La realtà è davvero tutta matematizzabile? E se anche fosse possibile trovare una legge matematica per ogni cosa, questa spiegherebbe davvero la realtà, o ne sarebbe solo un modello parziale, capace di cogliere solo una delle sue tante sfaccettature? Con queste domande ci avviamo alla conclusione. Ti anticipo, caro lettore, che sarà un finale aperto, perché non ho la risposta definitiva. È piuttosto un sentore, un presentimento, un’impressione. Perciò mi avvarrò delle parole di altri per esprimere questo mio pensiero finora solo abbozzato… Mi arrampicherò – a fatica – sulle spalle dei giganti (uno in particolare) per proporre una riflessione a Te, che stai leggendo questo articolo spinto dalla curiosità e che, ormai giunto alla fine, ti starai chiedendo dove voglia andare a parare.
Negli stessi anni in cui Pareto si accingeva a proporre nuove leggi matematiche in seguito alle sue osservazioni ortofrutticole, in Francia si leggevano le opere di un filosofo destinato ad essere insignito del premio Nobel per la letteratura. Henri Bergson, con le sue riflessioni sul concetto di tempo, rivoluzionò un’Europa dominata dal Positivismo, e assestò un colpo netto alle fondamenta del pensiero scientifico e di una visione del mondo basata su meccanismi numerici. Egli sosteneva che la scienza non fosse l’unica lente per comprendere la realtà, che ci fosse sempre qualcosa di irriducibile a mero numero. E quindi credeva che una chiave di interpretazione solamente scientifica ci facesse perdere il senso ultimo delle cose e un lato significativo anche di noi stessi in qualità di esseri umani. Queste affermazioni trovano in me un terreno fertile: pur ribadendo con fermezza la mia fiducia nel metodo scientifico e non rinnegando la mia formazione da “uomo di scienza”, sento nel profondo che ci stiamo perdendo qualcosa. Perciò ecco il mio invito a compiere il processo inverso rispetto a quello messo in atto da Pareto, che ha voluto introdurre la matematica in una disciplina fino ad allora puramente “umanistica”. A volte non bastano i numeri, serve lo spirito. O si può chiamarla anima, se più ti aggrada. Insomma, aderire ad un neoumanesimo, che promuova il ritorno dai dati alle emozioni, dai grafici alle storie e alle relazioni. Il bello è che non serve escludere una delle due facce, anzi. Sarà proprio dall’integrazione di questi due approcci che l’essere umano potrà fare il prossimo passo verso il futuro con maggiore conoscenza e consapevolezza. Un po’ come mi aveva raccontato – ormai una decina di anni fa – un monaco della comunità di Bose, il quale per rispondere ai miei dubbi sul contrasto tra scienza e fede mi disse: “Pensa ad un fiore. La scienza ci spiega in che modo i petali possano sbocciare seguendo un processo finemente regolato. Ma la fede, solo lei, può guidarci nell’ammirarne il mistero della sua inspiegabile bellezza”.

Bibliografia
[1] https://it.wikipedia.org/wiki/Principio_di_Pareto
[2] Rispoli, Fred & Zeng, Suhua & Green, Tim & Higbie, Jennifer. (2014). Even Birds Follow Pareto’s 80–20 Rule. Significance. 11. 10.1111/j.1740-9713.2014.00725.x.
[3]https://pablolacasia.medium.com/nature-and-the-80-20-universal-law-55948fd380de
[4] Chandrasekhar Arjun and Navlakha Saket 2019 Neural arbors are Pareto optimal Proc. R. Soc. B.28620182727
http://doi.org/10.1098/rspb.2018.2727
[5] O. Shoval et al. ,Evolutionary Trade-Offs, Pareto Optimality, and the Geometry of Phenotype Space. Science336,1157-1160(2012).DOI:10.1126/science.1217405
[6] Szekely P, Korem Y, Moran U, Mayo A, Alon U. The Mass-Longevity Triangle: Pareto Optimality and the Geometry of Life-History Trait Space. PLoS Comput Biol. 2015 Oct 14;11(10):e1004524. doi: 10.1371/journal.pcbi.1004524. PMID: 26465336; PMCID: PMC4605829.
[7] Cooper, L., Kang, S.Y., Bisanzio, D. et al. Pareto rules for malaria super-spreaders and super-spreading. Nat Commun 10, 3939 (2019). https://doi.org/10.1038/s41467-019-11861-y


Idem come sopra! Clicca qui per scoprirne di più su “Oltre Quella Siepe”!!!





